O!
Wanderers in the shadowed land
Despair not!
For though dark they stand,
All woods there be must end at last,
And see the open sun go past:
The setting sun, the rising sun,
The day’s end,
or the day begun.
For east or west all woods must fail.
J. R. R. Tolkien
You wake suddenly into a room you do not recognize.
This is not your bed.
Not your dresser.
Not your table.
The floor is rough-hewn wood. There are windows, but they are opaque. Light filters through, but nothing of the environment is visible.
You blink; you give yourself a moment to collect your thoughts, to remember.
Nothing comes.
You cautiously place a foot on the floor: cool, smooth, unfamiliar.
You tiptoe to the bedroom door.
The knob is large, brass. It looks ancient.
Above the door knob is a large brass plate. In it’s center there is a keyhole.
You bend down.
You close one eye and peer out.
What’s on the other side of the door?
Forest.
Forest forever, in every direction.
—–
For all our pretending…
Our intellectual strutting and preening, Our claims of omnipotence and rationality, our technological marvels and accomplishments…
The world is as uncertain as ever.
Whenever humanity’s understanding seems to encroach, fast and sure, onto the ends of the universe…
I try to remind myself of the scale of what we’re discussing.
I think about chess.
Chess has 16 pieces per player and 64 spaces.
The rules are defined.
Everything that needs to be known is known.
But there are more potential games of chess than there are subatomic particles in the universe.
It is infinite…
Despite its simplicity.
That’s been my biggest takeaway from studying game theory, risk, and COVID-19 these past few months:
The universe of unknown unknowns is impossibly vast…
Even if we understand the pieces.
Even if we think we understand how they all fits together.
I’ll give you one more example, before we head off into the forest in search of practical solutions…
Isaac Newton published the Philosophiæ Naturalis Principia Mathematica in 1687.
In it, he proposed three laws of motion:
1: An object either remains at rest or continues to move at a constant velocity, unless acted upon by a force.
2: The vector sum of the forces on an object is equal to the mass of that object multiplied by its acceleration.
3: When one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.
We’ve had 333 years to sit and think about these laws.
In that time, we’ve managed to invent computers with computational powers exceeding anything a human being is capable of.
With these tools – Newton’s Laws and our computers – we can precisely model the movements of bodies through space.
If we know their starting points and their velocities, we can perfectly plot the paths they’ll take.
We can literally calculate their future.
Of course, for each body we add into the problem, the calculations get more complex.
Eventually the system interactions become so intricate that it is impossible to calculate. It becomes chaotic, non-repeating.
Infinite.
How many bodies does it take for the problem to become incalculable?
With our 333 years of pondering Newton’s Laws?
With our super-powerful computers?
With all the human knowledge in all the world?
How many bodies?
Three.
—–
The door swings open.
It creaks, briefly, but the sound fades, absorbed into the thick, humid air.
Tress in every direction. They are massive, towering things.
Sun filters through the pine needles and dapples the ground like so many little spotlights. It’s not morning, but it’s hard to tell exactly where the sun is overhead.
The trees seem to come straight up to the door. There’s room to walk, but only just.
It should feel oppressive, like they are crowding you. Instead, it feels like you’ve interrupted a conversation.
You step out; the forest floor is soft and dry. As you look around, the door behind you swings shut.
You reach out, but it latches. You try to open it but it’s locked.
You take a breath and hold it.
The sweet taste of undergrowth, copper in the soil, a sense memory of an old Christmas tree.
Which way do you go?
—-
Complexity at the root of the universe.
So uncertainty is at the root of the universe.
So anxiety is at the root of the universe.
Anxiety is a perfectly normal reaction to the impossible task of trying to understand and predict a chaotic infinity of possibilities…
With a very limited, very non-infinite mind.
Despite that fact, we all have to wake up each day and do what needs to be done; to honor our commitments to ourselves and one another.
How do we navigate an uncertain world?
We choose the best path we can with the minimum amount of anxiety.
We use simple systems that allow us to quickly compare risks across categories.
We acknowledge our tendency to endlessly re-think, re-play, and re-consider our decisions…
And figure out how to let go.
We do the best we can, while minimizing our chances of losing too much.
In other words:
Heuristics…
Micromorts…
and MinMax Regret.
We discussed these concepts in an earlier post, so I won’t belabor them now.
Instead, what I want to do in this email is spell out…
Step by step….
Exactly how you can use these ideas to get a simple, practical estimate of how much risk you are willing to take on…
And to use that estimate to help you make the everyday decisions that affect your life.
—–
You walk until you get tired.
Something’s wrong, but you’re not sure what.
You don’t know where you are, so you could’ve chosen any direction at all.
You decided to simply go wherever the forest seems less dense, more open.
After a while (hours? days?) the trees have gotten further and further apart.
The slightly-more-open terrain has made walking easier.
You’re making more progress; towards what, you don’t know.
Every now and then you reach out to touch one of the passing trees; to trail your fingers along its bark.
The rough bumps and edges give you some textural variation, a way of marking the passing of time.
You look up. The sun doesn’t seem to have moved.
The sunlight still dapples. It’s neither hot nor cold. It isn’t much of anything.
Then you realize:
You haven’t heard a single sound since you’ve been out here.
Not even your own footsteps.
—–
Every good heuristic has a few components:
A way to search for the information we need…
A clear point at which to stop…
And a way to decide.
Let’s take each of these in turn.
Searching
We’ve discussed the “fog of pandemic” at length over the past few months.
With so much information, from so many sources, how do we know what to trust?
How do we know what’s real?
The truth is,
we don’t.
In the moment, it is impossible to determine what’s “true” or “false.” As a group we may slowly get more accurate over time. Useful information builds up and gradually forces out less-useful information.
But none of that helps us right here, right now – which is when we have to make our decisions.
So what do we do?
We apply a heuristic to the search for information.
What does this mean?
Put simply: set a basic criteria for when you’ll take a piece of information seriously, and ignore everything that doesn’t meet that criteria.
Here’s an example of such a heuristic:
Take information seriously only when it is reported by both the New York Times and the Wall Street Journal.
Why does this work?
1. These are “credible” sources that are forced to fact-check their work.
2. These sources are widely monitored and criticized, meaning that low-quality information will often be called out.
3. These sources are moderate-left (NYT) and moderate-right (WSJ). Thus, information that appears in both will be less partisan on average.
While this approach to vetting information might be less accurate than, say, reading all of the best epidemiological journals and carefully weighing the evidence cited….
Have you ever actually done that?
Has anyone you know ever done that?
Have half the people on Twitter who SAY they’ve done that, actually done that?
Remember:
Our goal is not only to make the best decisions possible…
It’s to decrease our anxiety along the way.
Using a simple search heuristic allows us to filter information quickly, discarding the vast majority of noise and focusing as much as possible on whatever signal there is.
You don’t have to use my heuristic; you can make your own.
Swap in any two ideologically-competing and well-known sources for the NYT and the WSJ.
Specifically, focus on publications that have:
– A public-facing corrections process
– A fact-checking process
– Social pressure (people get upset when they “get it wrong”)
– Differing ideological bents
– Print versions (television and internet tend to be too fast to properly fact-check)
Whenever a piece of information needs to be assessed, ask:
Is this information reported in both of my chosen sources?
If not, ignore it and live your life.
Stopping
When do you stop looking for more information, and simply make a decision?
This is a complicated problem. It’s even got it’s own corner of mathematics, called optimal stopping.
In our case, we need a way to prevent information overload…the constant sense of revision that happens when we’re buffeted by an endless stream of op-eds, breaking news, and recent developments.
I’ve written about this a bit in my blog post on information pulsing.
The key to reducing the amount of anxiety caused by the news is to slow it’s pulse.
If we control the pace at which information flows into our lives, we control the rate at which we need to process that information and reduce the cognitive load it requires.
My preferred pace is once a week.
I get the paper every Sunday. I like the Sunday paper because it summarizes the week’s news. Anything important that happened that week shows up in the Sunday paper in some shape or form.
The corollary is that I deliberately avoid the news every other day of the week.
No paper, no radio, no TV news, nothing online.
This gives me mental space to pursue my own goals while keeping me informed and preventing burnout.
Presuming that we’re controlling the regular pulse of information into our lives, we also need a stopping point for decision making.
Re-examining your risk management every single week is too much.
Not only is it impractical, it predisposes us to over-fitting – trying too hard to match our mental models to the incoming stream of data.
My recommendation for now is to re-examine your COVID risk management decisions once a month.
Once a month is enough to stay flexible, which I think is necessary in an environment that changes so rapidly.
But it’s not so aggressive that it encourages over-fitting, or causes too much anxiety.
We are treating our risk management like long-term investments.
Check on your portfolio once a month to make sure things are OK, but put it completely out of your head the rest of the time.
—-
You walk on, always following the less-wooded trail.
The trees are more sparse now.
It’s easier to walk, easier to make your way.
Eventually, you come to a clearing.
Your legs ache. You find a small log and sit down, taking a breath.
The air is warm. It hangs over you.
You breathe again.
Your eyes close.
Maybe you sleep.
You’re not sure.
None of it seems real.
Maybe you’re still dreaming.
But maybe you aren’t.
You could lie down, here. The ground is soft. There’s a place to comfortably lay your head.
It would be easy enough to drift away. It would be pleasant.
Or, you could push on.
Keep walking.
Maybe progress is being made.
Maybe it isn’t that far.
But maybe it is.
———
Deciding
We come now to the final stage of our process – deciding.
We’ve set parameters for how we’ll search for information…
And rules for how we’ll stop searching.
Now we need to use the information we take in to make useful inferences about the world – and use those inferences to determine our behavior.
This stage has a bit more steps to it.
Here’s the outline:
1. Get a ballpark risk estimate using micromorts for your state.
2. Play the common knowledge game.
3. Establish the personal costs of different decisions within your control.
4. Choose the decision that minimizes the chances of your worst-case scenario.
Let’s break each of these down in turn.
1. Get a ballpark risk estimate using micromorts for your state.
I’ve actually built you a handy COVID-19 Micromort Calculator that will calculate your micromorts per day and month based on your state’s COVID-19 data.
But if you don’t want to use my calculator, here’s how to do this on your own:
– Find the COVID-19 related deaths in your state for the last 30 days. Why your state? Because COVID-19 is highly variable depending on where you live.
– Find the population of your state (just google “My State population” and it should come right up).
(note: My COVID-19 Micromort calculator pulls all this data for you).
– Go to this URL: https://rorystolzenberg.github.io/micromort-calculator
– Enter the state’s COVID-19 deaths in the “Deaths” box.
– Enter the state population in the “People In Jurisdiction” box.
– In the “Micromorts per day” section put “30” in the “Days Elapsed” box.
Your calculator should look something like this:
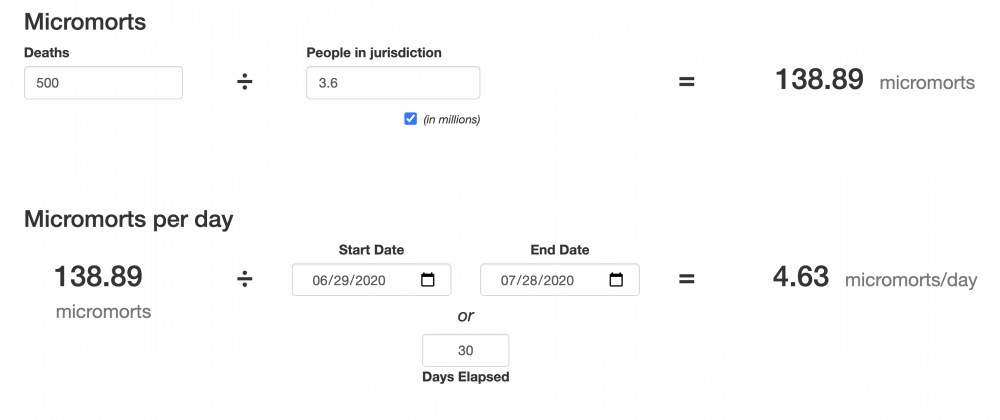 |
You’ve now calculated the average micromorts of risk per day in your state.
To compare this risk to other risks, situate your micromorts on this spreadsheet:
https://docs.google.com/spreadsheets/d/1xo3VrcDu6sMNGyykGKxgvRXv9kCwnFNAMHBoyc1y67Q/edit?usp=sharing
Take a look at the list and figure out how much risk we’re really talking about.
For example, the risk level in the image above is 4.63 micromorts – let’s round that to 5.
That means that I have about as much risk of dying from COVID-19 as I would of dying during a scuba dive, and more risk than I’d take on during a rock climb.
It’s also riskier than would be allowed at a workplace in the UK.
However, it’s less risky than going under general anesthetic, or skydiving.
Keep in mind, however, that these risks are per day.
Comparing apples to apples, I can ask:
“My COVID-19 risk is equivalent to the risk of going scuba diving every single day. Is that an acceptable risk level for me?”
2. Play the common knowledge game.
Now that we’ve got a rough estimate of risk, let’s think about other people.
You know.
Them.
Statistical risk matters, obviously.
But COVID-19 has a unique property:
It’s viral.
Literally.
If I’m riding a motorcycle, my risk does not increase if other people ride motorcycles, too.
For COVID-19? The actions of others have a big effect on my personal risk level.
This is where the common knowledge game comes in handy.
(You’ll recall our discussion of Common Knowledge games in previous emails, namely
The Beauty Contest, Missionaries, and Monty Hall.)
We don’t need to just weigh our own options…
We need to weigh what we think other people will do.
As an example:
My own state, Connecticut, has seen declining case numbers of COVID-19 for a few months now.
That gradual decline has led to a loosening of restrictions and a general increase in economic activity.
And that’s great!
But when it comes to sending our child to school next year, I’m still extremely worried.
Why?
Because I’m assuming that other people will see the declining case count as an indication that they can take on more risk.
What happens when people take on more risk in a pandemic?
Case numbers go up.
I ran into a similar issue early in the pandemic with regards to where I work.
I have a small office in a building downtown.
My room is private but other people share the space immediately outside my door.
Throughout the highest-risk days of the pandemic, when everyone else was staying home, I kept coming into the office to work.
Why?
Because everyone else was staying home.
They reacted rationally to the risks, and so my office building was empty.
Since it was only me, my personal risk remained low.
Now that risk levels are lower, people have started coming back to work…
Which means I am now more likely to work from home.
Why?
My actual risk remains the same, or higher, since more people have COVID-19 now than they did in the beginning.
But because case counts are declining, people feel safer and are more likely to come into the office, increasing my exposure.
Again:
Statistical risk matters…
But so does what other people do about that risk.
So.
While our micromort number is extremely useful, we need to run it through a filter:
How do I think the people around me will react to this level of risk?
What is “common knowledge” about our risk level?
What are the “missionaries” (news sources that everyone believes everyone listens to) saying, and how will that affect behavior?
Factor this into your decision-making.
—–
You keep moving.
Little by little, the ground becomes a trail, and the trail becomes a path.
Have other people been this way?
It’s hard to tell.
Maybe just deer.
But it’s a path. A way forward.
You think you detect some slight movement in the sun overhead.
Maybe, just maybe, time is passing after all.
With the path, there’s something to cut through the sameness – some way to judge distance.
Forward movement is forward movement.
You keep moving.
And then, something you never expected:
A fork.
Two paths.
One to the left, one to the right.
They each gently curve in opposite directions. You can’t see where they lead.
Something touches your back.
The wind.
Wind? you wonder. Was it always there?
Which way do I go?
—–
3. Establish the personal costs of different decisions within your control.
We’ve thought about risk, and we’ve thought about how other people will react.
Let’s take a moment to think about costs.
Every decision carries a cost.
It could simply be an opportunity cost (“If I do this, I can’t do this other thing…”)
Or the cost could be more tangible (“If I don’t go to work, I’ll lose my job.”)
One of the things that’s irritating about our discourse over COVID-19 is the extent to which people seem to assume that any action is obviously the right way to go…while ignoring it’s costs.
Yes, lockdowns carry very real costs – economic, emotional, physical.
Yes, not going into lockdowns carries very real costs – hospitalizations, deaths, economic losses.
Even wearing masks – something I am 100% in favor of – has costs. It’s uncomfortable for some, hampers social interaction, is inconvenient, etc.
We can’t act rationally if we don’t consider the costs.
So let’s do that.
Think through your potential outcomes.
You could get sick.
You could die.
There’s always that.
What else?
Maybe the kids miss a year of school.
What would the emotional repercussions be?
Or logistical?
Could you lose your job?
Lose income?
Have trouble paying bills?
What if there are long-term health effects?
What if the supply chain gets disrupted again…what if food becomes hard to find?
Think everything through.
Feel free to be dire and gloomy here…we’re looking for worst-case scenarios, not what is likely to happen.
Once you’ve spent some time figuring this out, make a quick list of your worst-cases.
Feel them emotionally.
We’re not looking to be most rational here. We’re getting in touch with our emotional reality.
We’re not saying, “What’s best for society? What do people want me to do?”
We’re asking:
Which of these scenarios would cause me the most regret?
Regret is a powerful emotion.
It is both social and personal. In many cases, we would rather feel pain than regret.
“Tis better to have loved and lost, than to have never loved at all.”
Rank your potential outcomes by “most regret” to “least regret.”
Which one is at the top?
Which outcome would you most regret?
THAT’S your worst-case scenario.
4. Choose the decision that minimizes the chances of your worst-case scenario.
Once you know:
– your rough statistical risk (micromorts)
– how other people will react (common knowledge game)
– and your own worst-case scenario (regret)
…You can start putting a plan in place to minimize your risk.
Here we are utilizing a strategy of “MinMax Regret.”
The goal is not to say “how can I optimize for the best possible scenario”….
…Because that’s difficult to do in such uncertain times.
It’s much easier to simply cover our bases and make sure that we do everything in our power to protect ourselves.
Thinking about your worst case scenario from Step 3, what can you do to ensure it doesn’t happen?
What stays? What goes?
Restaurants?
Visiting your parents?
Play dates for the kids?
What are you willing to give up in order to ensure the highest regret scenario doesn’t happen?
My own worst-case scenario?
Getting someone in a high risk category (like my Mom, or my son, who has asthma) sick.
What am I willing to give up to avoid that?
Eating at restaurants is out…
But we’ll get take out and eat outside.
Business trips are out. Easy choice.
I wear a mask.
I haven’t visited my mom, even though we miss her.
Can’t get her sick if we don’t see her.
But I visited my grandmother by talking to her through her window, with a mask on.
I’m not saying these decisions are objectively right or wrong…
But they were consistent with my goal:
Avoid the regret of getting the vulnerable people I love sick.
Once you’ve thought this through…
What’s my current risk?
How will other people react?
What’s my worst case scenario?
What am I willing to give up to minimize the possibility of that happening?
…Set up some ground rules.
What you’ll do, what you won’t.
What you’ll avoid, what you’ll accept.
And then don’t think about it at all until next month.
Give yourself the unimaginable relief…
Of deciding….
And then?
Forgetting.
—–
How long has it been?
Time seems to have stopped.
Or perhaps, moved on.
You keep walking, mostly as a way of asserting control.
My choice. Keep walking.
The path curved for a bit, then it straightened back out.
Slowly, but surely, it got wider and wider…the edges of the forest on either side drifting further and further apart.
It was like a curtain drawing back.
Your eyes were on the road, but as you look up now you realize….
You’re not in the forest anymore.
You’re not even on the path.
It’s open, all around.
Wide, impossibly wide. The sky and the earth touch each other.
The horizon is everywhere.
You’re glad you kept walking.
You’re glad you didn’t stop.
All woods must fail, you think.
As long as you keep walking.










